Trie
Trie 是用于维护一个字符串集合,判断某字符串是否在集合中出现的数据结构。
Trie 又叫字典树,就像它的功能一样,用于维护一个“字典”,其中存储若干字符串。
实际上,Trie 是一种前缀数据结构。不同字符串的相同前缀在 Trie 上是相同的部分。
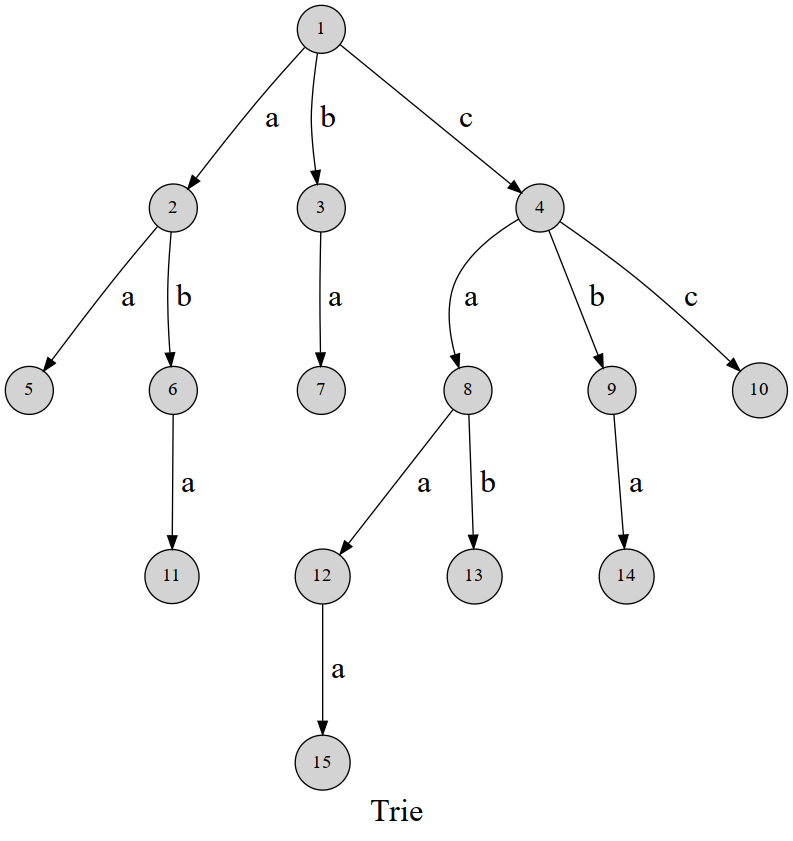
形式化而言,对于一个字符串 $S$,$S[i]$ 是 Trie 上第 $i+1$ 层的节点(因为所有字符串首字符不尽相同,所以需要一个公共根节点)。在 Trie 上,$S[i]$ 的父节点是 $S[i-1]$。
插入:
插入 $S$,从根节点出发,先访问根节点的 $S[1]$ 儿子,再访问 $S[1]$ 的 $S[2]$ 儿子,依次往复,直至插入 $S[|S|]$。在插入过程中,若对应儿子节点为空,则新建节点;若经过的所有点均存在,则在 $S[|S|]$ 对应节点的计数数组加 $1$,表示 $S$ 出现次数加 $1$。
查询:
询问 $S$ 是否出现。与插入类似,在访问到 $S[|S|]$ 过程中,若出现空节点则说明未出现;反之还要判断对应计数数组(因为可能是某个出现的字符串的前缀而不是整个字符串)。
01-Trie:
01-Tire 即用于存储 01 串的 Trie。
例:给定 $n$ 个数 $a_i$,求任意两数异或和的最大值。
对于一个给定数 $a_i$,考虑如何选择另一个 $a_j$ 使得 $a_i\oplus a_j$ 最大。
首先,长度不变情况下,比较数值大小,等价于比较字典序。所以要“贪心”地使最高位尽可能地大(在 $01$ 串中,即为要尽可能地为 $1$)。
所以从最高位开始,若 $a_i$ 对应位为 $0$,则 $a_j$ 尽可能为 $1$;反之为 $0$。那么在 01-Trie 上从 $a_i$ 的二进制表达的最高位开始,访问与 $a_i$ 相反的对应位即可。
时间复杂度:$O(n\log n)$。
因为每个数都要在 01-Trie 上求一遍,单次时间复杂度为 01-Trie 的深度,而 01-Trie 深度即为 $a_i$ 的二进制位数。