平衡树
平衡树是一种特殊的二叉搜索树。
定义:
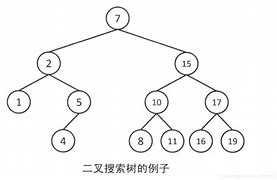
二叉搜索树是一种二叉树的树形结构,其定义如下:
- 空树是二叉搜索树。
- 若二叉搜索树的左子树不为空,则其左子树上所有点的附加权值小于其根节点的值。
- 若二叉搜索树的右子树不为空,则其右子树上所有点的附加权值大于其根节点的值。
- 二叉搜索树的左右子树均为二叉搜索树。
二叉搜索树上的基本操作所花费的时间与这棵树的高度成正比。
查找最值:
二叉搜索树上的最小值为二叉搜索树左链的顶点,最大值为二叉搜索树右的顶点。
查找元素:
设当前二叉搜索树子树的根为 root。
- 若 root 为空,返回
false。 - 若 root 的权值等于
value,返回true。 - 若 root 的权值大于
value,递归左子树。 - 若 root 的权值小于
value,递归右子树。
插入元素:
设当前二叉搜索树子树的根为 root。
- 若 root 为空,创建一个新节点插入元素。
- 若 root 的权值等于
value,该节点的权值对应的计数数组加 $1$。 - 若 root 的权值大于
value,递归左子树。 - 若 root 的权值小于
value,递归右子树。
删除元素:
先查找元素,若存在元素,设对应节点为 root。
- 若 root 权值对应的计数数组大于 $1$,则减 $1$。
- 若 root 为叶子节点,直接删除。
- 若 root 只有一个儿子的节点,返回这个儿子。
- 若 root 有两个非空子节点,用左子树的最大值替代它(swap 即可),再删除该节点。
求元素的排名:
排名的一个等价定义:比 $x$ 小的数的个数/比 $x$ 大的数的个数 $+1$(具体题目具体分析)。
在查找元素的过程中累加左子树的大小之和(同时累加节点的计数数组)即可。
查找排名为 k 的元素:
比 $x$ 小的元素个数为 $k-1$。设 $count$ 为当前节点对应的计数数组的值。
- 若左子树的大小大于等于 $k$,递归左子树。
- 若左子树的大小小于 $k-count$,则该元素在右子树中。
- 若其左子树的大小在区间 $[k-count,k-1]$ 中,则该元素为子树的根节点。
平衡树:
朴素二叉搜索树的时间复杂度均为 $O(h)$,在极限数据下,为 $O(n)$。
但是二叉搜索树树形态不唯一,这也就使得寻求一种 $h$ 更小更稳定的二叉搜索树成为了优化的核心道路。
平衡树即是指树高平衡的二叉搜索树,平衡树同样不唯一,根据不同的平衡策略可得不同的平衡树。
根据平衡方式可分为:旋转平衡、重构平衡、自平衡等。
平衡树均使得单次操作的时间复杂度为 $O(\log n)$,即使得树高均衡在 $O(\log n)$。但根据不同的平衡规则,部分平衡树为均摊时间复杂度而不是稳定时间复杂度。
在算法竞赛中使用较广的平衡树有:Treap(分为无旋 Treap(FHQ-Treap) 和带旋 Treap,通常 Treap 单指带旋 Treap,但无定论,还是要结合上下文)、Splay、替罪羊树、笛卡尔树。
其中 Splay 更多地被应用于 LCT(一种动态树)以及用于维护序列而不是值。替罪羊树和笛卡尔树相对使用较少,替罪羊树是一种基于重构的平衡树,笛卡尔树作为一种特殊形态的平衡树(本质是特殊的 Treap)其具有唯一性,在部分题目中对理解更加形象,但由于和单调栈没有本质区别,所有笛卡尔树具有可替代性。