莫队
普通莫队是一个基于分块的离线解决静态区间询问问题的算法。
但莫队算法扩展性极强,具有许多扩展莫队算法,
定义:
设询问区间为 $[l_i,r_i]$。对原序列索引分块。将询问区间离线后以 $l_i$ 所在块的编号为第一关键字,$r_i$ 为第二关键字升序。
对于每个询问 $[l_i,r_i]$ 的答案,由 $[l_1,r_1]$ 扩展而来,每次用 while 暴力移动 $l,r$ 指针。
此时,升序后的 $[l_i,r_i]$ 呈现,同一块内的 $l_i$ 对应的询问 $[l_i,r_i]$ 视作一个整体,共有 $\frac nt$ 个块。在一个块内的 $r$ 最多移动 $n$ 次(因为同一块内的 $r$ 升序,最多从 $1$ 移动到 $n$。在同一个块内 $l$ 每次扩展最多移动 $t$ 次。同时,从一个块的右端点询问的 $l$ 向下一个块的左端点的 $l$ 扩展时,$l$ 最多移动 $2t$,$r$ 最多移动 $n$。
综上:处理完 $m$ 个询问,$l,r$ 指针的总移动次数为:$O(\frac{n^2}{t}+mt)$。
当 $t=\frac{n}{\sqrt m}$ 时,时间复杂度最优为:$O(n\sqrt m)$。
一般认为 $n,m$ 同阶,所以直接取 $\sqrt n$。
上述只是考虑了指针移动次数。每次指针移动都要一次更新操作的时间复杂度。根据更新的复杂度不同,莫队的时间复杂度不同。
扩展:
关于四个循环位置的讨论:
莫队区间的移动过程,就相当于加入了 $[1,r]$ 的元素,并删除了 $[1,l-1]$ 的元素,因此:
- 对于 $l\leq r$ 的情况,$[1,l-1]$ 的元素相当于被加入了一次又被删除了一次,$[l,r]$ 的元素被加入一次,$[r+1,+∞)$ 的元素没有被加入。这个区间是合法区间。
- 对于 $l=r+1$ 的情况,$[1,r]$ 的元素相当于被加入了一次又被删除了一次,$[r+1,+∞)$ 的元素没有被加入。这时这个区间表示空区间。
- 对于 $l>r+1$ 的情况,那么 $[r+1,l-1]$(这个区间非空)的元素被删除了一次但没有被加入,因此这个元素被加入的次数是负数。
代码中四个 while 循环一共有 $4!=24$ 种排列顺序,不妨设第一个为移动 $l$,那么只考虑 $12$ 种,剩下 $12$ 种对称。
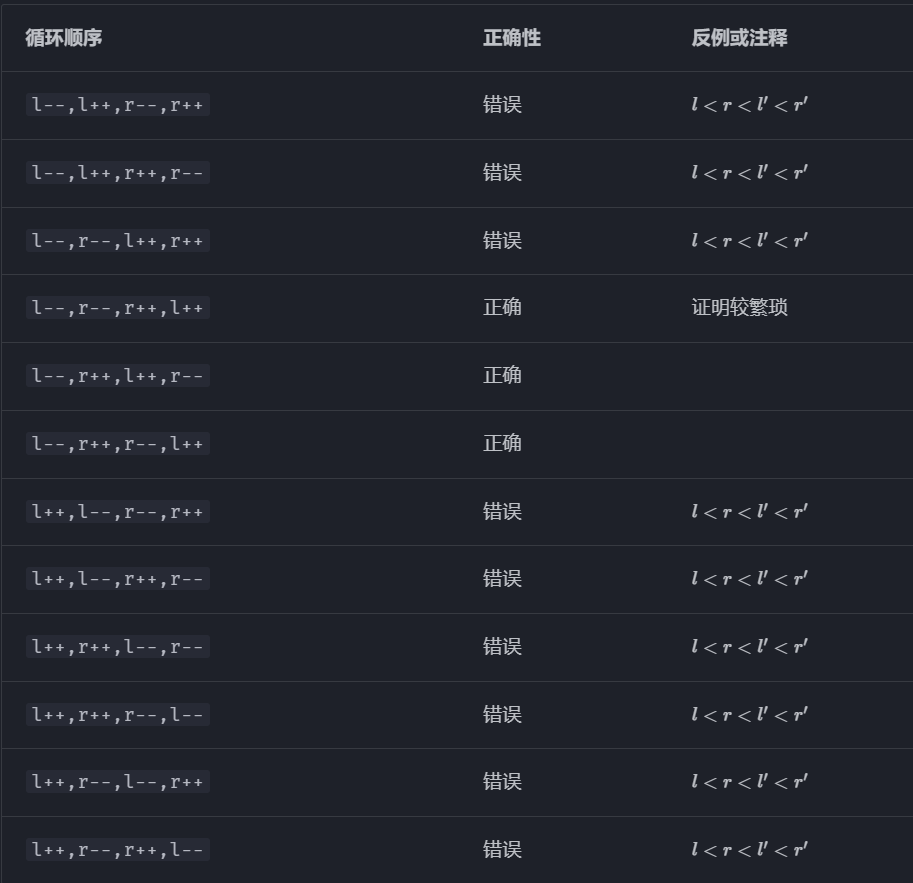
优化:
奇偶化排序:对奇数块内的询问的 $r$ 进行升序,对偶数块内的询问的 $r$ 进行降序。
这是很自然的,因为按原本的排序方式,每次进入一个新块时,r 都会从最大值降到最小值,再又升到最大值。这当然是不优的。
当然,这并不能改变复杂度,只是一个常用的有效的常数优化。