咕咕咕
0%

数据结构（三）

发表于 分类于
本文字数： 2k 阅读时长 ≈ 2 分钟

分块

分块是优美的暴力，但却并不是暴力。

常见分块为根号分块，一种基于根号均衡的根号算法。

在数据结构问题中，一般使用的为序列分块。

根号均衡：

$a\times b=n$，$\min\lbrace a,b\rbrace\leq \sqrt n$.

$a+\frac na\geq 2\sqrt n$

定义：

序列分块。

将原序列按 $t$ 为块长，划分成 $\frac nt$ 块。

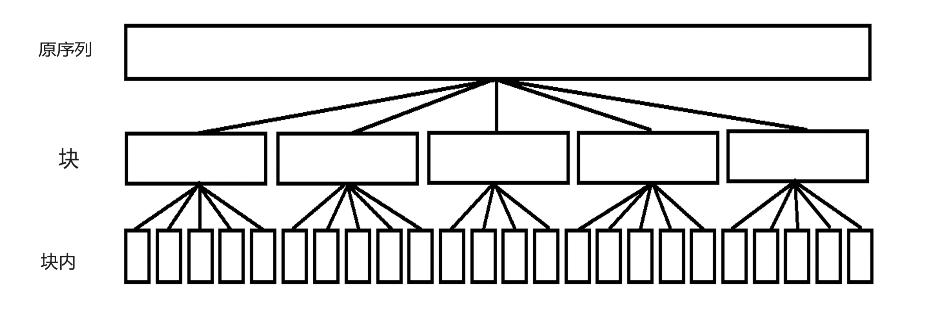
性质：

对于一个区间 $[l,r]$，一定可以拆分成：

  • 块的三部分：$l$ 到 $l$ 所在块的右端点；$l$ 所在块的下一块到 $r$ 所在块的上一块；$r$ 所在块的左端点到 $r$。
  • 特殊情况：$l,r$ 在同一块内。

对于块的三部分，一个块为一个整体，共有 $O(\frac nt)$ 个块，$l$ 和 $r$ 的块内元素共有 $O(t)$ 个。同样的，$l,r$ 在同一块内，元素个数为 $O(t)$ 个。$r$ 的块内元素共有 $O(t)$ 个。同样的，$l,r$ 在同一块内，元素个数为 $O(t)$ 个。

分（建）块：

枚举块的编号，遍历块的范围内元素以维护整块信息即可。

1
2
3
4
5
6
7
int bh(int x){return (x-1)/t+1;}//计算 x 所在的块的编号
int left(int x){return (x-1)*t+1;}//计算第 x 个块的左端点
int right(int x){return min(n,x*t);}//计算 x 个块的右端点

For(i,1,bh(n))
    For(j,left(i),right(i))
    	block[i].sum+=a[j];

注意一点：$n$ 是序列的右端点，但不一定是整块的右端点，要小心处理。体现在代码中，计算块的右端点时，和 $n$ 取 $\min$。

询问：

以区间求和为例分析，若维护整块的和，散块暴力累计。则单次询问时间为 $O(t+\frac nt)$。当 $t=\sqrt n$ 时，$O(t+\frac nt)$ 取得最小值，为 $O(2\sqrt n)$。所以一般块长设为 $\sqrt n$。

但是具体题目具体分析。由于不同题目限制不同，所得时间复杂度也不尽相同，所以块长也会做相应调整。

1
2
3
4
5
6
7
8
9
10
11
12
13
int query(int l,int r){
    int i;
    int res=0;
    For(i,bh(l)+1,bh(r)-1) res+=block[i].sum;
    if(bh(l)==bh(r)){
        For(i,l,r) res+=a[i]+block[bh(i)].tag;
    }
    else{
        For(i,l,right(bh(l))) res+=a[i]+block[bh(i)].tag;
        For(i,left(bh(r)),r) res+=a[i]+block[bh(i)].tag;
    }
    return res;
}

修改：

与询问一致，同样是散块暴力，整块整体维护。

但是此时存在一个问题：修改时维护了整块的整体的答案，但是整块内的信息并未得到维护，而在之后的询问中，询问到散块信息时，是需要整块内的信息的，所以这里需要借助和线段树一样的懒标记。

进行区间修改时，维护懒标记的信息。需要用到散块信息时，则将懒标记下传，维护散块信息。后重新维护整块信息。

笔者将下传标记维护散块信息写作 down，重新维护整块信息写作 up，两个过程一同视作块的重构过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void down(int l,int r,int v){
    int i;
    For(i,left(bh(l)),right(bh(r))) a[i]+=block[bh(l)].tag;
    block[bh(l)].tag=0;
    For(i,l,r) a[i]+=v;
}
void up(int x){
    int i;
    block[x].sum=0;
    For(i,left(x),right(x)) block[x].sum+=a[i];
}
void update(int l,int r,int v){
    int i;
    For(i,bh(l)+1,bh(r)-1)
        block[i].tag+=v,block[i].sum+=v*t;
    if(bh(l)==bh(r)){
        down(l,r,v);
        up(bh(l));
    }
    else{
        down(l,right(bh(l)),v);
        up(bh(l));
        down(left(bh(r)),r,v);
        up(bh(r));
    }
}

当然，对于维护可标记永久化的信息，使用标记永久化也可（就比如上文中的区间求和）。

扩展：

例题讲解：

分块入门-咕咕咕-LibreOJ数列分块入门

值域分块：