搜索 | 咕咕咕

搜索

也就是对状态空间进行枚举，通过穷尽所有的可能来找到最优解，或者统计合法解的个数。

搜索的基本概念：

状态：定量的描述一个唯一确定的情况。

状态转移：从一个状态转移到另一个状态的过程，涉及状态上信息的修改。

搜索树：跳过相同状态后，每一个状态视作一个结点，一个状态转移到另一个状态之间视作一条边。

搜索的基本形式：

（本文讨论的 DFS 和 BFS 更多地考虑实际问题的搜索，而非图论上的 DFS 和 BFS。对于图论上的 DFS 和 BFS 具有更多更有趣的性质，将在后续中讨论）

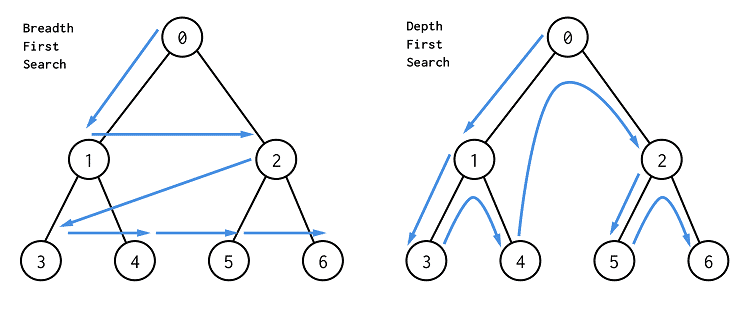
DFS（深度优先搜索）：

在搜索中，DFS 表现为使用递归函数枚举所有解空间。以函数参数作为状态。递归至找到解后返回。体现在搜索树上便是深度优先。

例1：

给定 $10$ 个数，选出 $3$ 个十进制位各不相同的数且和最大。

void dfs(int x,int sum){
    if(x>3){
        if(check(b[1],b[2],b[3])) ans=max(ans,sum);
        return ;
    }
    For(i,1,10){
        if(!vis[i]){
            b[++cnt]=a[i];
            vis[i]=1;
            dfs(x+1,sum+a[i]);
            vis[i]=0;
            cnt--;
        }
    }
}

BFS（宽度优先搜索）：

在搜索中，BFS 表现为使用队列枚举所有解空间。以队列元素作为状态。不断入队出队至找到解后终止。体现在搜索树上便是宽度优先。

同样解决例 1：

struct node{
    int x,sum;
    int a[4],b[3];
};
queue<node> q;
while(q.size()){
    auto now=q.front();
    if(now.x==3){
        ans=max(ans,now.sum);
        continue;
    }
    q.pop();
    For(i,1,10){
    	For(j,1,now.x) if(now.a[j]!=i&&check(a[i],now.b[j])){
            auto cur=now;
            cur.x++;
            cur.a[cur.x]=i;
            cur.b[cur.x]=a[i];
            cur.sum+=a[i];
            q.push(cur);
        }
        if(!now.x){
            auto cur=now;
            cur.x++;
            cur.a[cur.x]=i;
            cur.b[cur.x]=a[i];
            q.push(cur);
        }
    }
}

两种搜索方式在遍历解空间角度，仅仅是实现方式不同，一个使用栈（递归栈）一个使用队列，实现功能完全相同。

DFS 和 BFS 的比较：

在普遍的教学中，一般以迷宫问题作为 DFS 和 BFS 的引入问题。

那么就来看看迷宫问题：

例 2：

给定一个 $n\times m$ 的迷宫，$0$ 表示通路，$1$ 表示障碍求从 $(1,1)$ 到 $(n,m)$ 的最短路径。

DFS 实现：

void dfs(int x,int y,int z){
    if(x==n&&y==m){
        ans=min(ans,z);
        return ;
    }
	For(i,0,3){
        int X=dx[i]+x,Y=dy[i]+y;
        if(!vis[X][Y]&&maze[x][y]=='0'){
            vis[X][Y]=1;
            dfs(X,Y,z+1);
            vis[X][Y]=0;
        }
    }    
}

BFS 实现：

struct node{
    int x,y,z;
};
void BFS(){
    queue<node> q;
    while(q.size()){
        auto now=q.front();
        if(now.x==n&&now.y==m){
            ans=now.z;
            return ;
        }
        q.pop();
        For(i,0,3){
            int X=now.x+dx[i],Y=now.y+dy[i];
            if(maze[X][Y]=='0'){
                q.push({X,Y,now.z+1});
            }
        }
    }
}

观察两者，比较两者的不同。

DFS 需要添加 vis，要求递归过程中不能走回头路（走过的路），因为 DFS 代表一条路走到黑是典型的“不撞南墙不回头”。若允许走回头路，最直接的问题就是在两个状态之间来回横跳，陷入死循环。
BFS 不严格需要添加 vis，且 BFS 过程中终点第一次出队即为最短路径。因为 BFS 过程是将新状态加入队尾，在迷宫问题中满足每次路径只会增加不会减少或不变，且增量相等（都为 $1$）。而初始状态只有一个 $0$，所以 BFS 过程中的任意时候，队列的路径长度中只会有 $2$ 种值且小的在前，大的在后。也就说，出队的路径长度为单调不减且在有限个状态后一定会增。那么就一定会达到最短路径。所以不严格需要添加标记数组，只是会让无用的状态数大量增加。根据以上结论，其实可以发现，BFS 在状态转移增量恒为 $1$ 的问题中，第一次找到的解即为最优解。

对于标记数组，因为迷宫问题中，状态转移增量恒为 $1$，所以走过再走一遍的路只会让答案增大。

同时：

DFS 的标记数组需要回溯，为单独一条路径服务。
BFS 的标记数组不需要回溯，为全体路径共用。（注意：此条关于 BFS 标记数组的性质是因为状态转移增量为 $1$（状态转移增量相同也可视为 $1$）。而不是因为转移增量为正。若仅满足转移增量为正，不足以支撑所有点共用一个标记数组）

DFS 就像一个人独自找答案，不能同时尝试多种方法；BFS 就像一群人分别找答案，在同时尝试不同方法。

综上，可以发现：BFS 在状态转移增量恒为 $1$ 的问题中，第一次找到的解即为最优解且时间复杂度和空间复杂度均为 $O(nm)$ 因为每个点只会被入队一次。而 DFS 在最坏情况下仍会遍历全体解空间导致时间复杂度呈指数级。

而增量不恒为 $1$ 的情况下，BFS 就不能体现以上性质，因为队列中的解不呈单调不减的情况了。也就不能体现和 DFS 相比的优越性了。

DFS 和 BFS 均为搜索算法，仅仅是搜索角度不同。但一般提到搜索，均指 DFS。而 BFS 往往只作为在转移增量恒为 $1$ 的问题中求最小解。

这就是 BFS 在一般问题中标记数组不能共用导致的，在 BFS 的队列中存着若干状态，而每个状态均需要一个标记数组，那么空间复杂度便达到了状态数的平方，这是许多问题不能接受的。

而 DFS 不同，在 DFS 递归到某一层考虑当前函数内层，只存在一个状态，vis 仅为当前状态服务，也就只需要一个标记数组，那么空间复杂度便仅仅是状态数。

addition:

在例 $1$ 中，不用添加 vis。因为在例 $1$ 的搜索过程中不会出现走到某一条解路径重复走一个走过的状态，即：无环（DAG）。例 $2$ 却会，即：有环。

存储路径信息：

由于 DFS 采用栈存储既往状态，所以如果要求具体解的方案，只要把栈中状态依次取出即可。

而 BFS 不存储深度信息，只存储同一宽度的状态，自然就是不能得到到初始状态的方案，若是要求方案，就需要额外储存了。

这本身就是由深度和宽度而决定的，其实算不上什么优点或缺点，只是恰好实际中往往更需要求方案（即深度信息），而不是宽度信息，如果说现在有一题要求输出比最优解小 1 的状态，那么，DFS 就比不上 BFS 了。

DFS：

按深度递归，某一时刻状态数：$O(depth)$。

BFS：

按宽度递归，某一时刻状态数：$O(weight)$。

一个猜想：因为 DFS 只需使用到函数递归（递归本身便是一种栈），而不用像 BFS 那样用到数据结构 queue，更适合入门学习，所以更多地采用 DFS 写搜索而不是 BFS。

优化：

剪枝：

可行性剪枝：

若当前情况已经不符合题意则可以直接返回，而不需要走到头。

如例 $1$ 中，若搜索的第二个数已经不满足和第一个数匹配，那就没有必要继续搜索第三个数了。

最优性剪枝：

若当前情况已经劣于已经找到的最优解时，直接返回。

如例 $2$ 中，若当前搜到的路径已经比 $ans$ 大了，就不用继续搜了。

搜索顺序剪枝：

虽然从某种意义上说，这仅仅是“骗过了数据”。

但是不可否认的是大多情况下，改变搜索顺序可以优化搜索效率。

如例 $1$ 中，若从最大的数开始向小的数搜索，那么效率显然更优。

Alpha-Beta：

为一种固定化的剪枝手段。

可自行了解。

略。

人类智慧：

以上剪枝策略只是形式化的剪枝策略。还可以利用人类智慧来进行剪枝：

极端法：考虑极端情况，如果最极端的情况都不满足，那一定不满足。
调整法：通过对子树的对比剪掉重复子树和明显不是最优的子树。
数学方法：比如在图论中借助连通分量，数论中借助模方程的分析，借助不等式的放缩来估计下界等等。

在实际应用中，往往需要选手自行根据题目发扬剪枝艺术。并没有一个固定的写法。

搜索状态的设计：

虽然搜索是遍历所有的解空间。但对于不同的状态设计，会呈现出不同的解空间。

以例 $1$ 为例，前文中设计是状态为选到第 $x$ 个数，和为 $sum$。将结果直接写在状态中，那么状态总数即为 $3\times sum$ 的所有可能值。而如果换一种状态设计：$\lbrace a_1,a_2,…,a_{10}\rbrace$ 其中 $a_i=1/0$ 表示第 $i$ 个数是否被选，状态数总数为 $2^{10}$，结果可以通过状态另外求出。

同时，在实际应用中，根据题目需要，还可以去掉一些无用的状态（剪枝）。

就如例 $1$，容易得到 $10$ 个数选 $3$ 只有 $\binom{10}{3}$ 种有用的状态。

不同的状态定义所形成的搜索树也不尽相同。

通过巧妙的状态定义，也可更好地解决问题。

同时，虽然搜索是遍历所有解空间，但是时间复杂度并不是解空间大小。也不是状态数大小。因为在的搜索过程中，访问到搜索树上同一个节点时，会继续往下考虑，将搜过的内容再搜一遍。

仍以例 1 为例。看这样一组数据：

2 3 3 2 1 4

对于 $(3,5)$ 这样的状态，能被多少个状态转移而来：$(2,2),(2,3),(2,1),(2,4)$。

而 $(3,5)$ 接下去的状态，$(2,2),(2,3),(2,1),(2,4)$ 都会再考虑一遍。

记忆化搜索：

记忆化搜索是一种通过记录已经遍历过的状态的信息，从而避免对同一状态重复遍历的搜索实现方式。

与其说是记忆化搜索，笔者更愿称之为记忆化递归。通过递归将一个大的问题变成一个个小问题，然后拼接起来。

例 3：

给定 $10$ 个数，选出 $3$ 个数的和小于 $1000$ 且最大。

容易发现仅仅是三个数要满足的限制变了，所以按例 $1$ 的 DFS 写法把 check 函数变一变即可。但是这样无法记忆化的。因为它每一个状态维护的是到起点的结果，而不是到终点。既然是到终点，那么 $sum$ 就不能直接维护，而是要通过函数递归返回值求得：

int dfs(int x){
    if(x>3) return 0;
    int res=0;
    For(i,1,n){
        if(!vis[i]){
            vis[i]=1;
            if(dfs(x+1)+a[i]<1000)
            	res=max(res,dfs(x+1)+a[i]);
            vis[i]=0;
        }
    }
    return res;
}

记忆化搜索因为使用以往搜到是结果，那么就要保证现在到这一步时确确实实能按以往的结果做选择。如果到这一步之前的选择的不同影响了后续的可选择性，那自然是不能用之前的结果的，也就是满足“子问题”。

所以上述代码中仅仅用 $(x)$ 描述状态并不是一个子问题。所以需要对状态设计进行修改，使得一个状态描述确确实实是一个子问题。

状态可以修改为 $(i,x)$ 最后选的一个数是第 $i$ 个数，已经选了 $x$ 个数。因为限制死了后续只能选择 $i+1,i+2,…n$ 中的数，那么就保证了遇到 $(i,x)$ 这个状态时，后续的可选择性是一致的。

因为只需要在一般搜索的基础上进行记录状态结果的行为，所以记忆化搜索算是一种优化思想。体现在代码上也并不复杂。

核心变为如何存储状态信息：

一般而言，若状态信息并不复杂（主要是数值不大）那么便可以直接用数组进行存储，将状态信息记录为数组下标。

int dfs(int _i,int x){
    if(_i>n) return ;
    if(x>3) return 0;
    if(vis[_i][x]) return mem[_i][x];
    int res=0;
    For(i,_i+1,n)
        if(dfs(i+1,x+1)+a[i]<1000)
        	res=max(res,dfs(i+1,x+1)+a[i]);
    vis[_i][x]=1;
    mem[_i][x]=res;
}

BFS 因为不搜到底，并不能利用已经到过的状态（就算状态是到过的，但是没有它到终点的结果）。所以 BFS 不存在记忆化搜索的写法。

事实上，问题的 $sum$ 一般都会比较大，不能作为数组下标存储。但是我们可以使用 map 将状态和状态的结果视作一个映射，存起来。

因为记忆化搜索确保了每个状态只访问一次，它也是一种常见的动态规划实现方式。

addition：

为什么要用例 $3$ 记忆化而不是例 $1$？

因为例 $1$ 根本无法简单地记忆化，因为例 $1$ 的后续的选择是和前面所有选的具体数字是有关的，而不是仅通过和就可以判断是否能选的（例 $3$ 中的 check 只关心和的大小，不关心具体选的数；例 $1$ 中的 check 需要关心所有选择的数）。同一个状态描述对应的不同实际状态的后续操作不尽相同。比如例 $1$ 中，选择 $2,3$ 或 $1,4$ 都对应 $(3,5)$ 的状态描述，但在选择第三个数时，他们的选择是不一样的。

所以例 $1$ 中的状态不足以支撑记忆化的过程。

但是观察会发现，其实不是状态不行，而是状态描述不行。选择的数在例 $1$ 中是要考虑到状态描述中去的，那么在状态描述中加上选择的数即可。但是这样产生的问题就是状态不易存储。

我们需要更巧妙的状态描述。本文不再赘述。

双向搜索：

同时双向搜索：

同时从起点和终点开始搜索。往往采用 BFS 实现。

把起点和终点都加入初始队列。

在扩展过程中，把由起点扩展的一系列点标记为 $1$，把由终点扩展的一系列点标记为 $2$。当 $1$ 能扩展到 $2$，或 $2$ 能扩展到 $1$ 时，表示找到解。

由于起点和终点交题前进，所以对于起点和终点，各自的深度只有原规模的一半，那么状态规模的增长也只有原来的一半。

meet in middle：

将原问题划分成两部分分别处理，后将两部分的结果合并。meet in middle 往往用于处理序列问题，把序列划分成左右两部分。

例 4：

给定 $40$ 个数，求选出若干个数的和不超过 $10^9$ 的方案数。

直接对 $40$ 个数搜索所有解的时间复杂度为：$O(2^{40})$。

若将序列划分成两个长度为 $20$ 的序列，首先单独处理的时间复杂度为：$O(2^{20})$。

之后，对于左半部分的某一个解，在右半部分中找到之和不超过 $10^9$ 的方案数。即为在若干个数中求不超过某值的数的个数，可以使用二分解决（upper_bound）。

总时间复杂度：$O(20\times 2^{20})$。

一般而言，决定是否能双向搜索的均为两部分信息是否能合并。

若原问题状态规模为 $O(a^{k})$，双向搜索状态规模降为 $O(a^{\frac{k}2})$。

A*：

A* 是基于 BFS 的改进。

定义从 $x$ 到起点的距离为 $g(x)$，从 $x$ 到终点的距离为 $h(x)$，$x$ 的估价函数为 $f(x)$。初始起点入队，每次从队列中取出估价函数最小的一个元素。$h(x)$ 称为启发函数，因为无法直接获取从 $x$ 到终点的距离，所以对 $h(x)$ 采用的往往是一个估价量，要求不超过真实距离，且越接近真实距离，越优。

迭代加深搜索：

每次限制递归层数的 DFS。

每进行一次 DFS，递归深度限制增大 $1$。

避免了 DFS 的递归层数过多；也避免了 BFS 在同一时刻状态数过多。

但存在重复搜索前缀的缺点，不过由于搜索树的规模增长一般为指数，深度增大一层的数据规模可能会超过前面所有层的数据规模之和。所以影响并不是那么大。

IDA*：

A* 和迭代加深的结合。

01 BFS：

在前文中，提到 BFS 主要用于解决边权为 $1$ 的最短路径问题。但是注意到 BFS 过程中队列内是有两个距离值的，队尾比队首大 $1$，边权为 $1$ 时每次扩展加在队尾。如果边权还存在 $0$ 的话，则加在队首。其它部分与 BFS 完全相同。

优先队列 BFS：

在前文中，提到 BFS 如果处理边权不为 $1$ 的问题，那便没有第一次出队即为最小值的性质了。究其本质，是因为队列内元素不呈现单调性了。

但是可以“强行”让队列内元素呈现单调性。即：采用优先队列替换队列实现。

但若是边权存在负值，那仍然不满足第一次出队时为最小值（不能使用 vis 数组）

原因显然。

Dancing Links：

解决精确覆盖问题和重复覆盖问题的高效搜索算法。

采用十字链表加上优秀的剪枝实现。

略。

启发式搜索：

贪婪最佳优先搜索：

$h(x)=0$ 的 A*，也就是优先队列 BFS，也可以说是 Dijkstra。

模拟退火：

它是一种基于概率的搜索算法，模拟固体物质的退火过程。它以一定的概率接受比当前解更差的解，以避免陷入局部最优。它的估价函数是 $f(n)= e^{-\frac{ΔE}{T}}$，其中 $ΔE$ 表示新解和旧解的能量差，$T$ 表示温度参数。它的优点是能够跳出局部最优，缺点是参数的选择比较难，收敛速度慢。

遗传算法：

蚁群算法：

粒子群优化算法：

番外：

对抗搜索：

这里的对抗搜索是指双人进行对抗博弈。

博弈原理：

存在先手必胜策略，当且仅当存在一种策略使得不存在后手必胜策略。
存在后手必胜策略，当且仅当无论先手怎么操作，都有后手必胜策略。

一般状态设计为 dfs$(x,…y)$ $x=1/0$ 表示先手/后手；$y=1/0$ 表示必胜/必败；返回值为 $1/0$ 表示是否存在。参数其它部分用于描述局面信息。

dfs$(x,…,1)=$dfs$(x\oplus 1,…0)$ 与之和。
dfs$(x,…,0)=$dfs$(x\oplus 1,…1)$ 或之和。

Attention：

因为搜索其本身时间复杂度上界很高，以及剪枝没有严格时间复杂度证明，所以近年来的算法竞赛中搜索相关问题的出现次数大大减少，除非题目本身明确上界也能通过，否则不会是搜索问题。