咕咕咕
0%

数据结构（二）

发表于 更新于 分类于
本文字数： 5.3k 阅读时长 ≈ 5 分钟

线段树

千呼万唤始出来。

线段树是算法竞赛中最常用的、应用最广的用来维护 区间信息 的数据结构。

线段树可以在 $O(\log n)$ 的时间复杂度内实现单点修改、区间修改、区间查询等操作。

定义：

线段树将每个长度不为 $1$ 的区间划分成左右两个区间递归求解，把整个线段划分成一个树形结构。

设 $x$ 的管辖区间为 $[l,r]$，则 $x$ 的左儿子的管辖区间为 $[l,mid]$，$x$ 的右儿子的管辖区间为 $[mid+1,r]$。

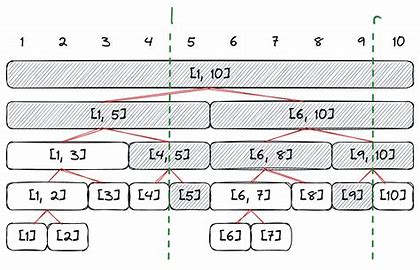
在实际应用中，采用二进制编码的方式表示树上的结点：

设当前结点为 $x$，则左儿子为 $x<<1$，右儿子为 $x<<1|1$。

（用一个结构体维护结点蕴含所有信息，把左右儿子的序号直接存进结构体也是一种常见写法，但是笔者看来更适合之后的动态开点线段树）

因为这样的堆式存储使得部分结点就算在线段树没有实际左右儿子，但是同样会占用数组内存，所以线段树总结点个数为 $2^{\lceil{\log n}\rceil+1}-1$。当 $n=2^x+1$ 时，结点树数取得最大值：$4n-5$。所以一般线段树开 $4n$ 的空间。

性质：

对于一个 $[x,y]$ 一定能被拆分成 $O(\log n)$ 个线段树上结点所表示的区间并。

这是支持线段树完成 $O(\log n)$ 实现区间操作的基本原理。

证明：

在线段树上递归时，考虑第一个中点位于 $[x,y]$ 之间的区间 $[l,r]$。此时，$[x,y]$ 便可以依 $mid$ 划分为两部分：$[x,mid]$ 和 $[mid+1,y]$。$mid$ 是 $[l,mid]$ 的右端点，$mid+1$ 是 $[mid+1,r]$ 的左端点。

先考虑 $[mid+1,r]$ 中划分 $[mid+1,y]$ 的情况。

容易发现，$[mid+1,r]$ 中划分 $[mid+1,y]$ 的第一个区间长度是 $\leq y-mid$ 的最大 $2$ 的整数幂。之后的递归也是同理，所以 $[mid+1,y]$ 就被划分成了若干个严格递减的 $2$ 的整数幂长度的区间，容易发现，这个至多是 $O(\log n)$ 级别的。$[l,mid]$ 划分 $[x,mid]$ 同理。

综上：一个 $[x,y]$ 一定能被拆分成 $\log n$ 个线段树上结点所表示的区间并。

（本文以线段树维护区间和，区间加示例）

建树：

按定义所规定的管辖区间递归建树即可。用子结点信息更新父节点信息。

1
2
3
4
5
6
7
8
9
10
void build(int t,int l,int r){
    int mid=l+r>>1;
    if(l==r){
        tr[t].sum=a[l];
        return ;
    }
    build(t<<1,l,mid);
    build(t<<1|1,mid+1,r);
    push_up(t);
}

区间询问：

在具体的线段树代码实现中，不唯一，不局限。只要本质相同即可。

下面以笔者代码分析：

1
2
3
4
5
6
7
int query(int t,int l,int r,int x,int y){
    int mid=l+r>>1,res=0;
    if(x<=l&&r<=y) return tr[t].sum;//返回信息
    if(x<=mid) res+=query(t<<1,l,mid,x,y);//返回左儿子的信息
    if(y>mid) res+=query(t<<1|1,mid+1,r,x,y);//返回右儿子的信息
    return res;
}

当递归到的结点所在区间完全包含于询问区间，则直接返回结点信息。

询问区间在递归时，可以改成前文中的 $[x,mid]$ 和 $[mid+1,y]$，不影响结果。因为之后递归的结点区间若完全包含于 $[x,mid]$ 或 $[mid+1,y]$ 则一定也完全包含于 $[x,y]$。

单点修改：

线段树的单点修改较区间修改更复杂，下面先考虑单点修改。

（单点修改是区间修改的子集，若线段树一定能支持某类操作的区间修改，则一定能支持单点修改，反之不然）

从线段树的根节点开始，递归到 $[x,x]$ 所在结点。后回溯更新祖先结点信息。

1
2
3
4
5
6
7
8
9
10
void update(int t,int l,int r,int x,int v){
    int mid=l+r>>1;
    if(l==r){//l=r一定满足l=x=r
        tr[t],sum+=v;
        return ;
    }
    if(x<=mid) update(t<<1,l,mid,x,v);
    else update(t<<1|1,mid+1,r,x,v);
    push_up(t);
}

子结点信息更新父节点信息：

一般将此操作写作 push_up 作为一个单独的函数出现。

1
2
3
void push_up(int t){
    tr[t].sum=tr[t<<1].sum+tr[t<<1|1].sum;
}

区间修改：

类比区间询问，将修改区间 $[x,y]$ 拆分成线段树上 $O(\log n)$ 个区间。把修改的信息标记到这个区间上。但是这时候就能发现，这样并没有维护住线段树的定义信息。标记的区间的儿子结点的信息没有更新，标记的区间的父节点的信息也没有更新。可要让所有结点的信息都完成更新，则需要修改 $O(n)$ 个结点的信息，这是不能接受的。

标记永久化：

修改操作和询问操作是紧密联系在一起的，如果不支持询问的操作，那么修改的支持便毫无意义。

以区间加，单点查询为例：

因为单点查询时，必然递归经过所有包含单点的区间。所以可以把修改的信息和初始信息分开考虑，将标记就固定在修改到的区间上。那么在查询时，把递归路径上经过的区间上的标记信息累计起来即可。

但是对于区间询问，就有所不同，因为区间询问时不会递归到拆分之后的区间的后代结点，而若修改的标记标记到了某个拆分之后的区间的后代结点上，就会对答案产生影响。所以对于区间询问，永久化的标记同样要作用于祖先结点。查询时只会查询到标记的某一个祖先结点而不会有多个，所以不影响答案。

同时，标记永久化具有较大的局限性，例如在信息不可直接叠加值时，便不具有可永久化的性质。比如：区间赋值；同时维护区间加和区间乘。

标记永久化也有它的优点，例如：不用像懒标记那样下传标记，常数较小；在可持久化线段树中，对区间修改标记永久化，空间复杂度可以少乘 $O(\log n)$ 。

懒标记：

对于懒的解释：延迟下传。

在前文考虑维护住线段树定义时，是因为要保证其它点也满足线段树的定义。但是，

修改操作和询问操作是紧密联系在一起的。试想，如果在后续的询问操作中，没有用到这里修改操作所涉及的点，那么是否还需要去把所有点都更新？

因此，秉持不用不管的原则，只有当询问操作递归经过这个区间时，才将这个区间上的标记信息下传更新子结点的信息。至于父结点信息，在修改操作递归到这个区间的过程中直接修改即可。

注意，懒标记的标记与标记永久化的标记不同，懒标记的标记是与线段树结点的信息结合起来的，是需要通过懒标记去修改结点上的信息的。而标记永久化的标记是与线段树结点的信息独立的。也就是标记永久化过程中的结点信息是不变的（始终为建树时的信息）而懒标记过程中的结点信息是会随着懒标记的下传而更新的（当前结点的懒标记下传后，懒标记信息清空，结点信息更新）

懒标记具有较强的扩展性，可以维护更多信息。但是需要维护的内容更多，代码更长。

懒标记中，懒标记下传函数一般写作 push_down，结点信息更新一般不写成函数，笔者写作 eval。

1
2
3
4
5
6
7
8
9
10
void eval(node &t,int l,int r,int v){
    t.tag+=v;//维护懒标记信息
    t.sum+=v*(r-l+1);//维护结点信息
}
void push_down(int t,int l,int r){
    int mid=l+r>>1;
    eval(tr[t<<1],l,mid,tr[t].tag);//懒标记下传左儿子
    eval(tr[t<<1|1],mid+1,r,tr[t].tag);//懒标记下传右儿子
    tr[t].tag=0;
}

懒标记还有一个要注意的点，何时 push_down。

根据前文：“不用不管”，那么就是说只要递归到了这个区间，那就要 push_down。所以在递归前就 push_down 且任何修改和询问操作，只要递归到了这个点，就应该 push_down，一般应用中，push_down 的位置置于 if 后面，递归前面。

下面是完整的区间加、区间和的懒标记线段树代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include<bits/stdc++.h>
#define int long long
#define For(i,a,b) for(i=a;i<=b;i++)
#define FOR(i,a,b) for(i=a;i>=b;i--)
#define pb push_back
using namespace std;
const int N=1e5+10;
int a[N];
struct node{
	int sum,tag;
};
struct sege{
	node tr[N<<2];
	void push_up(int t){
		tr[t].sum=tr[t<<1].sum+tr[t<<1|1].sum;
	}
	void eval(node &t,int l,int r,int v){
		t.tag+=v;
		t.sum+=v*(r-l+1);
	}
	void push_down(int t,int l,int r){
		int mid=l+r>>1;
		eval(tr[t<<1],l,mid,tr[t].tag);
		eval(tr[t<<1|1],mid+1,r,tr[t].tag);
		tr[t].tag=0;
	}
	void build(int t,int l,int r){
		int mid=l+r>>1;
		if(l==r){
			tr[t].sum=a[l];
			return ;
		}
		build(t<<1,l,mid);
		build(t<<1|1,mid+1,r);
		push_up(t);
	}
	void update(int t,int l,int r,int x,int y,int v){
		int mid=l+r>>1;
		if(x<=l&&r<=y){
			eval(tr[t],l,r,v);
			return ;
		}
		push_down(t,l,r);
		if(x<=mid) update(t<<1,l,mid,x,y,v);
		if(y>mid) update(t<<1|1,mid+1,r,x,y,v);
		push_up(t);
	}
	int query(int t,int l,int r,int x,int y){
		int mid=l+r>>1,res=0;
		if(x<=l&&r<=y) return tr[t].sum;
		push_down(t,l,r);
		if(x<=mid) res+=query(t<<1,l,mid,x,y);
		if(y>mid) res+=query(t<<1|1,mid+1,r,x,y);
		return res;
	}
}tree;
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	int n,m,i,l,r,v,op;
	cin>>n>>m;
	For(i,1,n) cin>>a[i];
	tree.build(1,1,n);
	while(m--){
		cin>>op;
		if(op==1){
			cin>>l>>r>>v;
			tree.update(1,1,n,l,r,v);
		}
		if(op==2){
			cin>>l>>r;
			cout<<tree.query(1,1,n,l,r)<<'\n';
		}
	}
	return 0;
}

扩展：

动态开点线段树：

值域线段树：

可持久化线段树：

线段树合并：

线段树分裂：

线段树优化建图：

线段树分治：

zkw 线段树：

势能线段树：

李超线段树：