数据结构（一）

树状数组

树状数组是一种基于二进制位性质的类树形结构，可以 $O(\log n)$ 进行单点修改，$O(\log n)$ 进行前缀询问的数据结构。

性质：

$lowbit(x)=x\And-x$

$lowbit(x)$ 定义为非负整数 $x$ 在二进制表达下，最低位的 $1$ 及其后面的 $0$ 构成的二进制数。同时也是最大的整除 $x$ 的 $2$ 的整数幂。

证明：

在计算机中，负整数的二进制表示，为正整数的二进制取反后加 $1$ 。

也就是保留从后往前第一个 $1$ 后将其它位置取反。

所以 $x\And-x$ 即为 $x$ 在二进制表达下，最低位的 $1$ 及其后面的 $0$ 构成的二进制数。

定义：

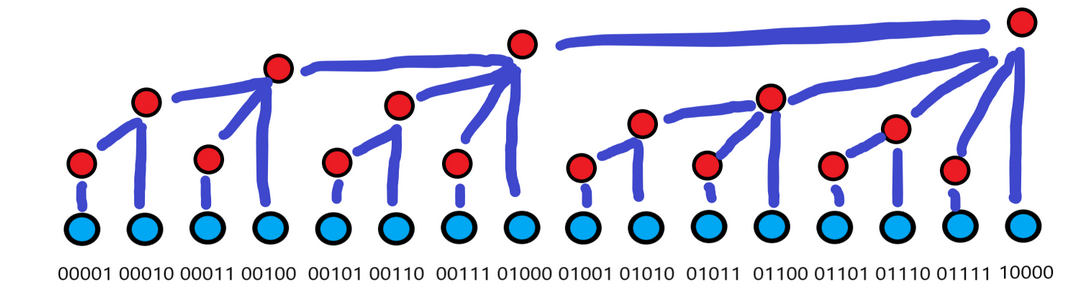
树状数组定义了 $tr[x]$ 表示区间 $[x-lowbit(x)+1,x]$ 的信息和。我们称这个区间为 $x$ 的管辖区间。

询问：

那么对于一个前缀区间 $[1,x]$，一定能拆分成 $x$ 的二进制上 $1$ 的位数个 $tr[x]$ 的和。

例如 $[1,5]$ 可以划分成 $[5,5]$ 和 $[1,4]$ 两个。

$5:[100+1,101] 4:[000+1,100]$

那么将这二进制位数个 $tr[x]$ 相加就实现了 $O(\log n)$ 的前缀查询，因为二进制位数是 $O(\log n)$ 级别的，而且是不大于 $O(\log n)$ 的。

每一次 $-lowbit(x)$ 即可得到下一个区间。

修改：

要修改的是 $x$ 位置的单点值，但是我们需要修改不止一个 $tr[x’]$。因为是否修改 $tr[x’]$ 是取决于 $tr[x’]$ 是否覆盖了 $x$。

解释 $1$：

$tr[x’]$ 所管辖的区间为 $[x’-lowbit(x’)+1,x’]$。当 $x’-lowbit(x’)\leq x\land x\leq x’$ 时，tr[x’] 覆盖了 $x$。此时 $x’$ 满足，$x’$ 除 $lowbit(x’)$ 外的高位为 $x$ 的前缀，且 $lowbit(x’)$ 为 $1$ 的这一位 $x$ 为 $0$。

这样的 $x’$ 可以通过 $x$ 开始不断 $+lowbit(x)$ 得到。

解释 $2$：

根据树状数组的树形结构，$tr[x’]$ 覆盖了 $x$ 当且仅当 $x’$ 是 $x$ 的祖先结点，那么不断跳父节点就可以得到 $x’$ 了，而跳父节点的操作，在树状数组上就是 $+lowbit(x)$。

每一次 $+lowbit(x)$ 都会变成下一个 $1$ 更高的第一个 $0$ 的位。所以时间复杂度同样是 $O(\log n)$ 的。

struct BIT{
    int tr[N],n;
    int lowbit(int x){
        return x&(-x);
    }
    void update(int x,int v){
        for(;x<=n;x+=lowbit(x)) tr[x]+=v;
    }
    int query(int x){
        int res=0;
        for(;x;x-=lowbit(x)) res+=tr[x];
        return res;
    }
}Bit;

扩展：

前缀 $\min/\max$：

若能理解树状数组的原理，便不难解决这个问题。

树状数组将前缀询问分成了 $O(\log n)$ 个独立的区间，那么只要是能够通过合并两个区间信息得到的大区间信息，都可以可以维护的。

单点修改则用修改后的信息更新 $O(\log)$ 个区间，那么是否支持修改为任意数呢？

答案是否定的。对于前缀 $\min$ 只能支持单点减的修改；对于前缀 $\max$ 只能支持单点加的修改。

因为树状数组修改是基于旧最值和新修改的值进行的更新，而最值不能依附于旧值，因为无法确定这个最值是否恰好是被修改的数。

区间询问：

树状数组本身维护的为前缀区间信息。然而若维护的信息是可差分的，即 $[l,r]$ 的信息可以通过 $[1,r]-[1,l-1]$ 得到，那么就可以利用树状数组支持区间询问。

区间修改：

同样的，若维护的信息是可差分的，那么将区间修改转化成单点加和单点减，即可实现区间修改。

区间询问+区间修改：

使用上述差分的方法，也只能仅支持区间询问或仅支持区间修改，不能同时支持区间询问和区间修改。

那么是否能使用树状数组同时支持区间询问和区间修改呢？

也是有可能可以的。

牢牢把握树状数组的本质：单点修改和前缀询问。树状数组本质是不能改变的，但是具体的询问和修改却可以依题目而变，所以可以尝试从修改和询问的性质入手。

以区间加和区间求和为例：

令 $b_i=a_i-a_{i-1}，$$\sum\limits_{i=l}^r a_i=\sum\limits_{i=l}^r\sum\limits_{j=1}^i b_j$

考虑每个 $b_j$ 的贡献，可得：$\sum\limits_{i=l}^r(r-i+1)\times b_i=(r+1)\times\sum\limits_{i=l}^rb_i-\sum\limits_{i=l}^rib_i$。

所以只要维护两个树状数组，一个维护 $b_i$，一个维护 $ib_i$，即可。

$b_i$ 已经是差分数组了，对 $b_i$ 的修改即为单点修改。

树状数组维护不可差分信息：

此部分数据结构功能对应线段树，但时间复杂度严格劣于线段树，选择性学习。

树状数组维护不可差分信息，依然是只能支持单点修改和区间询问，但单点修改和区间询问时间复杂度均为 $O(\log^2n)$。

区间询问：

对于区间询问 $[l,r]$ 同样是将区间拆分成若干个区间，只是现在不能拆到 $1$ 了，即拆分成的区间的范围不能小于 $l$。

因此：

$x-lowbit(x)<l$，将 $a[x]$ 合并即可，然后继续从 $tr[x-1]$ 考虑。直到 $x=l$，$a[x]$ 即为原序列，直接在原序列上维护即可。
$x-lowbit(x)\geq l$，正常考虑。

int query(int l,int r) {
    int ans=0;
    while(r>=l){
        ans=max(ans,a[r]);
        --r;
        for(;r-lowbit(r)>=l;r-=lowbit(r)) ans=max(ans,tr[r]);
    }
    return ans;
}

单点修改：

不可差分信息单点修改同最值（最值本身即为一种不可差分信息）。不能使用旧值更新新值。

但是，树状数组上，$x$ 的儿子的信息是没有发生变化的（也就依然是新值），所以先用儿子更新 $tr[x]$，再用修改的新值更新 $tr[x]$ 即可。同时，由于 $x$ 的新值会破坏它的所有父节点的信息，所以 $x$ 所有的父节点也都要用儿子更新一遍

void update(int x,int v) {
    a[x]=v;
    for (;x<=n;x+=lowbit(x)){
        tr[x]=a[x];
        for (v=1;v<lowbit(x);v<<=1) 
            tr[x]=max(tr[x],tr[x-v]);
    }
}

上述做法虽然是 $O(\log^2n)$ 的，但是很显然，其常数巨小，实际表现不一定会在所有情况下劣于线段树的 $O(\log n)$，而且代码量极短。

权值树状数组：

正常情况下，使用树状数组维护的是一个序列，而权值树状数组维护的则是问题的值域。原理与使用与普通树状数组无异，这里不再赘述。

这里只是引入这样将树状数组视作“计数器”维护值域的思想。

通常使用权值树状数组维护逆序对数量与全局第 $k$ 小。

树状数组二分：

例如：在保证 $a_i\geq 0$ 的情况下，求最小的 $x$ 满足 $\sum\limits_{i=1}^x a_i>y$。且要求多次询问和单点加。

树状数组$+$二分：

更形象的叫法应该是：树状数组套二分。那么就是在外层二分模型下，查询前缀和。同时维护单点加。

时间复杂度：$O(\log^2n)$。

虽然是 $O(\log^2n)$，但是实际表现却十分优先，许多情况下，并不比线段树上二分劣。

int l,r,mid;
l=1,r=n;
while(r-l>4){
    mid=l+r>>1;
    if(Bit.query(mid)>v) r=mid;
    else l=mid+1;
}
for(mid=l;mid<=r;mid++) if(Bit.query(mid)>v) break;

树状数组上二分：

更准确地这里应该是树状数组上倍增，但是一般而言倍增和二分可以互相转化，所以也无伤大雅。

从最高位开始，若这一位的管辖区间和加上已累加的超过了 $y$，则考虑下一位，否则就累加到答案中。最多考虑 $\log n$ 位。

时间复杂度：$O(\log n)$。

int ask(int v){
    int _log=0;
    while((1<<_log)<=n)  _log++;
    _log--;
    int i,x=0;
    FOR(i,_log,0)
    if(tr[x+(1<<i)]<=v){
        v-=tr[x+(1<<i)];
        x+=(1<<i);
    }
    return v+1;
}