旋转卡壳
概念
点集的直径:平面最远点对(一定是其凸包上的某两个极点)。
性质
- 各极点到其中一点的距离并不存在单调性。
- 但是各极点到一条极边的距离存在单峰性。
旋转卡壳
卡尺绕凸包旋转,其两边经过的点构成对踵点。
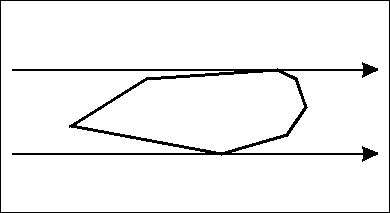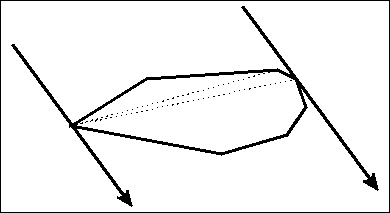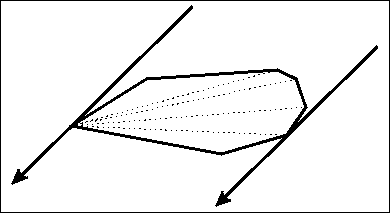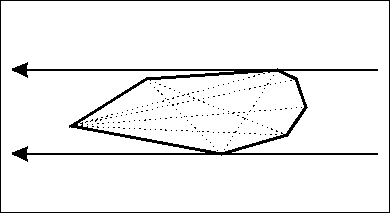
一个点的对踵点不好直接得出,且可能不止一个。但一条边的对踵点可以利用上页提到的单峰性找出。
卡尺的一条边逆时针经过各条极边时,另一条边对应的对踵点也是逆时针依次经过,因此二者可以通过双指针进行遍历。
卡尺旋转过程中一定存在某时刻其两边经过直径对应的两点。
算法流程
- 设定初始边指针 p,并找到其对踵点 q。
- p 指向下一条边。
- 如果 q 点到 p 边的距离小于等于 q 的下一个点到 p 边的距离,则 q 指向下一个点。
- 重复 3 直到找到 p 边的对踵点,更新答案。
- 回到 2。
此处的距离比较可转化为面积比较,从而可以使用叉积解决。
时间复杂度:$O(n)$。
应用
凸多边形间最大/小距离
重新定义“对踵点”:
以凸多边形某条边作为 y 轴,x 坐标最小的点。
在此定义下,该点依然是和该边组成叉积最大的点。
除此之外,算法流程与求点集直径一致。
凸多边形间最小面积/周长外接矩形
不论是最小周长还是面积的外接矩形,其一定有一条边与凸包的一条极边共线。
在旋转卡壳时,多维护方向上的两个极点即可。