半平面交
概念
半平面:有向直线左侧的区域。
半平面交:多个半平面的交集。
半平面交涉及直线均使用点向式表示。
性质:半平面交一定是凸集。
特别地,可以加入一个相当大的边界,将交集无穷大的情况转化为有边界,这样交集可以用一个凸多边形表示。
做法
法一:朴素算法
求出各直线的交点,判断各交点是否在所有平面内。
对满足条件的各点求凸包。
时间复杂度:$O(n^3)$。
法二:增量法;
每次用直线去切割当前的凸多边形。
时间复杂度:$O(n^2)$。
法三:排序增量法:
求凸包算法中,对点进行排序可以有效降低复杂度。
利用凸多边形各边方向向量的有序性,同样可以对各直线进行排序后求半平面交。
对于方向向量同向的直线,只需要考虑最左的一个。
维护过程
用双端队列维护当前的半平面交:
当加入一个新的半平时,可能有以下几种情况。
- 队尾的一些半平面变成冗余的,从队尾弹出。
- 队首的一些半平面变成冗余的,从队首弹出。
- 半平面交变成空集。
时间复杂度:$O(n\log n)$。瓶颈在于排序。
判断冗余
队尾/首两条直线的交点在新加入的直线右侧。
外边界
在加入外边界的前提下,半平面交中相邻各边逆时针旋转不超过 $180^\circ$。
当无解的情况出现时,新加入的直线与队首差。一定大于等于 $180^\circ$,并且会把队中除队首外的直线全部弹出。
因此,每加入一条新直线,弹出冗余半平面后与队尾比较,如果逆时针旋转大于等于 $180^\circ$,则交集为空。
此时,外边界的加入是必要的。
先处理队尾,再处理队首
当出现一个可以把队列里的点全部弹出去的向量(即队列里的所有点都在该向量的右侧),则我们必须先处理队尾,再处理队首。
原因如下:
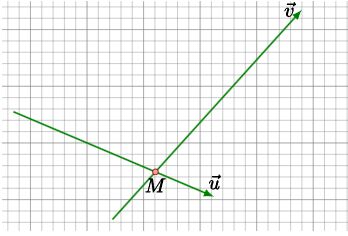
一般情况下,我们在队列里(队列顺序为 $\lbrace\vec u,\vec v\rbrace$)后面加一条边(向量 $\vec w$),会产生一个交点 $N$,缩小 $\vec v$ 后面的范围。
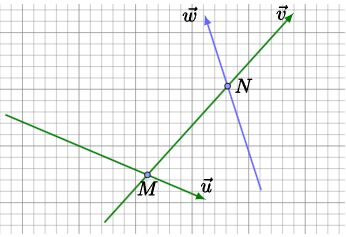
但是毕竟每次操作都是1一般的,因此可能会有把 $M$ 点 $\lceil$挤出去$\rfloor$ 的情况。
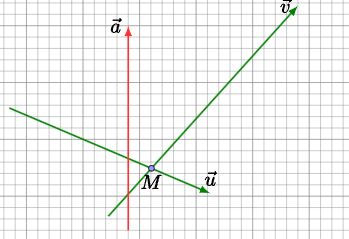
如果此时出现了 $\vec a$,使得 $M$ 在 $\vec a$ 的右侧,那么 $M$ 就要出队了。此时如果先处理队首,显然是扩大了范围。实际上 $M$ 点是由 $\vec u$ 和 $\vec v$ 共同构成的,因此需要考虑影响到现有进程的是 $\vec u$ 还是 $\vec v$。而因为我们在极角排序后,向量是逆时针顺序,所以 $\vec v$ 的影响更大一些。
就如上图,如果 $M$ 确认在 $\vec a$ 的右侧,那么此时 $\vec v$ 的影响一定不会队半平面交的答案作出任何的贡献。
而我们排除队首的原因是 当前直线的限制比队首大,这个条件的前提是队列里有不止两个直线,不然就会出现上面的情况。
所以一定要先排除队尾在排除队首。
交点在新加入直线上
队尾/首两条直线的交点在新加入的直线上时,一般不认为这时的队尾/首是冗余的,这样便可区分出交集面积为 0 与交集为空。
特殊情况:多条直线交于一点。
法四:分治法
时间复杂度:$O(n\log n)$。
$[l,r]$ 直线的半平面交是$[l,mid]$ 半平面交和 $[mid+1,r]$ 半平面交的交集。
核心在于实现 $O(n)$ 求两个凸多边形的交。
实现一:
使用法三求两个凸多边形半平面交得到凸多边形的交。
因为半平面交求出的交的边是有序的,所以合并 $[l,mid]$ 和 $[mid+1,r]$ 时,两个凸多边形都是有序的,那么使用法三维护的时间复杂度瓶颈即为维护双端队列的复杂度。为 $O(n)$。
实现二:
对两个凸多边形的顶点进行扫描线,对两相邻竖线之间的梯形求交。单次 $O(1)$。共 $O(n)$ 条竖线。