二维几何基础知识
浮点数与精度问题
特殊值
- +0.0 -0.0
- 1.0/0.0=+inf,1.0/-0.0=-inf
- nan,非数字,例如:$\sqrt{-2}$
- nan 除了 $\neq$ 时返回
true外,其它比较运算符均返回false
- nan 除了 $\neq$ 时返回
1.若问题能用整数解决则不用浮点数。
2.除非时限紧张,否则使用 long double。
3.减少数学库函数的调用。
4.进行浮点数比较时,加入容限(误差)eps。
点
using Point=complex<double>
- 横坐标(x):.real()
- 纵坐标(y):.imag()
优点:自带各种运算
缺点:慢
using Point=pair<double,double>
- 横坐标(x):first
- 纵坐标(y):second
优点:自带比较运算
缺点:自由度不高
struct Point {double x,y;}
- 横坐标(x):x
- 纵坐标(y):y
优点:自由度高
缺点:功能为零
向量
表示上和点一致,因为坐标系中一个点对应一个向量。
点积
$\vec{a}\cdot \vec b=a_xb_x+a_yb_y$
几何意义:$\vec a\cdot \vec b=|\vec a|\times |\vec b|\times \cos\theta$
- 向量的长度:$|\vec a|=\sqrt{\vec a\times \vec a}$
- 向量的夹角:$\cos \theta=\dfrac{\vec a\cdot \vec b}{|\vec a|\times |\vec b|}$
- 向量的投影:$|\vec a|\times cos\theta=\dfrac{\vec a\cdot \vec b}{|\vec b|}$
- 向量垂直:$\vec a\cdot \vec b=0$
叉积
$\vec a\times \vec b=(a_xb_y-a_yb_x)\hat k$
几何意义:$\vec a\times \vec b=|\vec a|\times |\vec b|\times \sin \theta \hat k$
- 平行四边形面积:$|\vec a\times \vec b|=|\vec a|\times |\vec b|\times |\sin \theta|$
- 向量平行:$\vec a\times \vec b=\vec 0$
- to-left 测试
to-left 测试
判断点 P 在有向直线 AB 左侧/右侧上。
$\begin{cases}\overrightarrow {AB}\times \overrightarrow{AP}>0& P\ 在有向直线\ AB\ 左侧\newline \overrightarrow {AB}\times \overrightarrow{AP}<0&P\ 在有向直线\ AB\ 右侧\newline\overrightarrow {AB}\times \overrightarrow{AP}=0& P\ 在有向直线\ AB\ 上\end{cases}$
向量逆时针旋转
$\vec a$ 逆时针旋转 $\theta$,$(a_x,a_y)\rightarrow(\cos\theta a_x-\sin\theta a_y,\sin\theta a_x+\cos\theta a_y)$
线段
struct segement{Point a,b;}
记录左右端点
判断点是否在线段上
- 点 P 在 AB 所在直线上:$\overrightarrow {PA}\times \overrightarrow{PB}=\vec 0$
- 点 P 在 AB 之间:
- $\overrightarrow{PA}\cdot \overrightarrow{PB}< 0$
- $\min(A_x,B_x)\leq P_x\leq\max(A_x,B_x)\ \land\ \min(A_y,B_y)\leq P_y\leq\max(A_y,B_y)$
判断两条线段是否相交
- 点 A 和点 B 在直线 CD 的不同侧
- 点 C 和点 D 在直线 AB 的不同侧
- 三点共线、四点共线特判
直线
斜截式
$y=kx+b$
截距式
$\dfrac{x}{a}+\dfrac{y}{b}=1$
一般式
$Ax+By+C=0$
点斜式
$y-y_1=k(x-x_1)$
两点式
$\dfrac{x-x_1}{x_2-x_1}=\dfrac{y-y_1}{y_2-y_1}$
点向式
直线上一点 P + 方向向量 $\vec v$ 表示一条直线。
求直线与点 A 的距离
$d=\dfrac{|\vec v\times \overrightarrow{PA}|}{|\vec v|}$
求点 A 在直线上的投影点 B
$\overrightarrow {OB}=\overrightarrow{OP}+\overrightarrow{PB}=\overrightarrow{OP}+\dfrac{|\overrightarrow{PB}|}{|\vec v|}\vec v=\overrightarrow{OP}+\dfrac{\overrightarrow{PA}\cdot\vec v}{\vec v^2}\vec v$
两直线交点
$\overrightarrow {OQ}=\overrightarrow{OP_1}+\dfrac{|\vec{v_2}\times \overrightarrow{P_2P_1}|}{|\vec{v_1}\times \vec{v_2}|}\vec{v_1}$
多边形
由点集描述。
- 一般按逆时针顺序
- 不一定满足凸性
- 注意第一个点与最后一个点的处理
多边形的面积
三角形的面积:$\dfrac{1}{2}|\vec a\times \vec b|$
多边形的面积:分解为若干三角形的面积
$S=\dfrac{1}{2}|\sum\limits_{i=0}^{n-1}\overrightarrow{OP_i}\times \overrightarrow{OP_{(i+1)\bmod n}}|$
判断点是否在多边形内
光线投影法
从该点引出一条射线,如果这条射线与多边形有奇数个交点,则该点在多边形内部,否则该点在多边形外部。
回转数法
回转数:面内闭合曲线逆时针绕过该点的总次数。
遵循非零规则:当回转次数为 0 时,点在曲线外部。
一种实现方法:计算相邻两边夹角(有方向)的和。
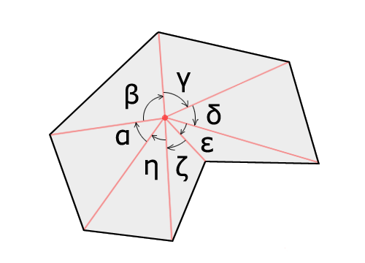
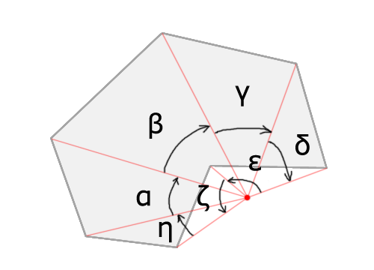
另一种实现方法:从该点引出一条射线,每经过一条自上而下穿过该射线的边,贡献 -1;每经过一条自下而上穿过该射线的边,贡献 +1。
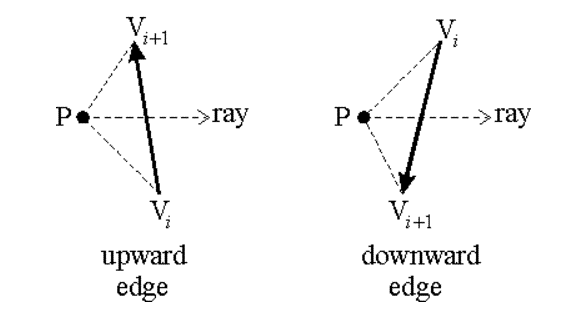
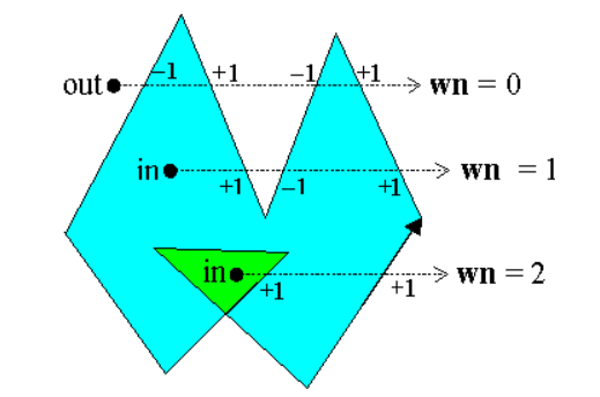
边界情况
- 点在多边形上,对于每条边特判。
- 引出射线交多边形于顶点,视作在在射线上侧(影响自下而上还是自上而下的判断)。
判断点是否在凸多边形内
n 次 to-left 测试
$O(n)$
二分
$O(\log n)$